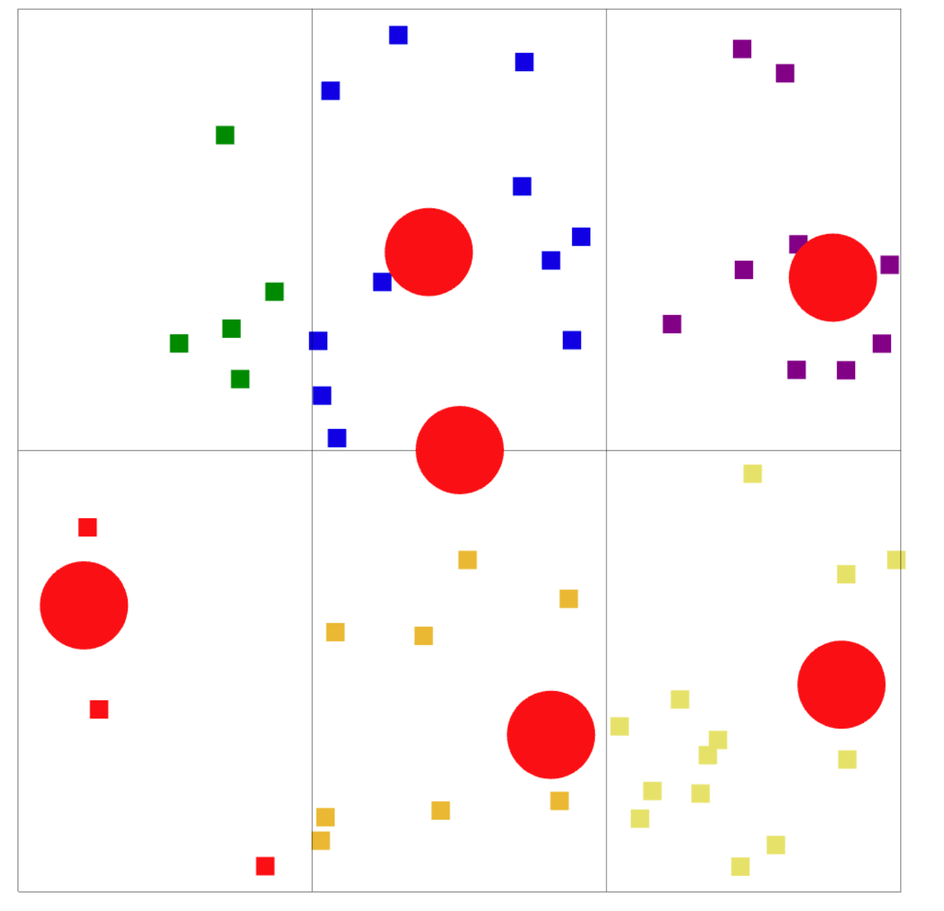
Centroids - Precursor to Normal Calculation in Point Clouds

This is a precursor to getting 3D centroids and then doing normal reconstruction for point clouds and therefore leading to light calculations.

Below shows whats been accomplished in this little bit of research.

What is a centroid?

In Point Clouds: The centroid of a group of points is calculated as the average of their coordinates, providing a central point that summarizes the location of the group.

Imagine this:

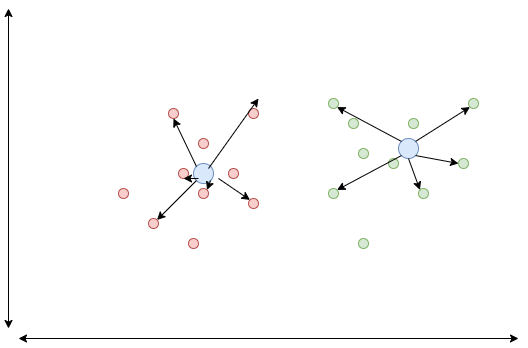
So once we have the centre points for local point clouds we can essentially constuct normals which can then subsequently be used in lighting calculations.

We can do some creative things to determine if the point is within the cloud or on the outer edges. To be discussed in later posts.

I have no idea if this will work but its a creative way to approach the normal issues for point clouds in 3JS.

Here is the code.

1import React, { useRef, useEffect } from 'react';
2import { Canvas, useFrame } from '@react-three/fiber';
3import * as THREE from 'three';
4
5function calculateAverages(positions, numPoints, boxSize) {
6    // Initialize section sums and counts
7    const sectionSums = Array(6).fill(null).map(() => ({ x: 0, y: 0, count: 0 }));
8  
9    const thirdBoxSize = boxSize / 3;
10    const halfBoxSize = boxSize / 2;
11  
12    // Loop through the positions
13    for (let i = 0; i < numPoints; i++) {
14      const x = positions[i * 3];
15      const y = positions[i * 3 + 1];
16  
17      // Determine xSection (left, middle, right)
18      let xSection;
19      if (x < -thirdBoxSize) {
20        xSection = 0; // Left
21      } else if (x < thirdBoxSize) {
22        xSection = 1; // Middle
23      } else {
24        xSection = 2; // Right
25      }
26  
27      // Determine ySection (bottom, top)
28      const ySection = y < 0 ? 0 : 1;
29  
30      // Calculate section index
31      const sectionIndex = xSection + ySection * 3;
32  
33      // Accumulate sums and counts
34      sectionSums[sectionIndex].x += x;
35      sectionSums[sectionIndex].y += y;
36      sectionSums[sectionIndex].count += 1;
37    }
38  
39    // Calculate averages for each section
40    const averages = sectionSums.map(({ x, y, count }) => {
41      if (count === 0) return { x: 0, y: 0 }; // Avoid division by zero
42      return { x: x / count, y: y / count };
43    });
44  
45    return averages;
46  }
47
48  function calculateSectionIndices(positions, numPoints, boxSize) {
49    const sectionIndices = new Array(numPoints);
50    const horizontalDivisions = 2; // Number of horizontal sections
51    const verticalDivisions = 3;   // Number of vertical sections
52    const horizontalStep = boxSize / horizontalDivisions;
53    const verticalStep = boxSize / verticalDivisions;
54  
55    for (let i = 0; i < numPoints; i++) {
56      const x = positions[i * 3];
57      const y = positions[i * 3 + 1];
58  
59      // Determine horizontal section
60      const horizontalSection = Math.floor((y + boxSize / 2) / horizontalStep);
61  
62      // Determine vertical section
63      const verticalSection = Math.floor((x + boxSize / 2) / verticalStep);
64  
65      // Ensure sections are within valid range
66      const clampedHorizontalSection = Math.min(horizontalDivisions - 1, Math.max(0, horizontalSection));
67      const clampedVerticalSection = Math.min(verticalDivisions - 1, Math.max(0, verticalSection));
68  
69      // Calculate section index
70      sectionIndices[i] = clampedHorizontalSection * verticalDivisions + clampedVerticalSection;
71    }
72  
73    return sectionIndices;
74  }
75  
76
77function Points({ numPoints, boxSize }) {
78  const pointsRef = useRef();
79  const velocities = useRef(new Float32Array(numPoints * 2));
80  const groupRef = useRef(null);
81
82  const colors = [
83    new THREE.Color("red"),
84    new THREE.Color("orange"),
85    new THREE.Color("yellow"),
86    new THREE.Color("green"),
87    new THREE.Color("blue"),
88    new THREE.Color("purple"),
89  ];
90
91  useEffect(() => {
92    const positions = pointsRef.current.geometry.attributes.position.array;
93    const colorsArray = pointsRef.current.geometry.attributes.color.array;
94
95    for (let i = 0; i < numPoints; i++) {
96      const x = Math.random() * boxSize - boxSize / 2;
97      const y = Math.random() * boxSize - boxSize / 2;
98      positions[i * 3] = x;
99      positions[i * 3 + 1] = y;
100      positions[i * 3 + 2] = 0;
101
102      velocities.current[i * 2] = (Math.random() - 0.5) * 0.01;
103      velocities.current[i * 2 + 1] = (Math.random() - 0.5) * 0.001;
104    }
105
106    const sectionIndices = calculateSectionIndices(positions, numPoints, boxSize);
107
108    for (let i = 0; i < numPoints; i++) {
109      const color = colors[sectionIndices[i]];
110      colorsArray[i * 3] = color.r;
111      colorsArray[i * 3 + 1] = color.g;
112      colorsArray[i * 3 + 2] = color.b;
113    }
114
115    pointsRef.current.geometry.attributes.position.needsUpdate = true;
116    pointsRef.current.geometry.attributes.color.needsUpdate = true;
117  }, [numPoints, boxSize, colors]);
118
119  useFrame(() => {
120    const positions = pointsRef.current.geometry.attributes.position.array;
121
122    for (let i = 0; i < numPoints; i++) {
123      positions[i * 3] += velocities.current[i * 2];
124      positions[i * 3 + 1] += velocities.current[i * 2 + 1];
125
126      if (positions[i * 3] <= -boxSize / 2 || positions[i * 3] >= boxSize / 2) {
127        velocities.current[i * 2] *= -1;
128      }
129      if (positions[i * 3 + 1] <= -boxSize / 2 || positions[i * 3 + 1] >= boxSize / 2) {
130        velocities.current[i * 2 + 1] *= -1;
131      }
132    }
133
134    const sectionIndices = calculateSectionIndices(positions, numPoints, boxSize);
135    const colorsArray = pointsRef.current.geometry.attributes.color.array;
136
137    for (let i = 0; i < numPoints; i++) {
138      const color = colors[sectionIndices[i]];
139      colorsArray[i * 3] = color.r;
140      colorsArray[i * 3 + 1] = color.g;
141      colorsArray[i * 3 + 2] = color.b;
142    }
143
144    pointsRef.current.geometry.attributes.position.needsUpdate = true;
145    pointsRef.current.geometry.attributes.color.needsUpdate = true;
146
147    const averages = calculateAverages(positions, positions.length / 3, 1);
148
149    if (groupRef.current) {
150        const children = groupRef.current?.children;
151
152        children.forEach((child, index) => {
153            const position = child.position;
154            const avg = averages[index];
155            position.x = avg.x;
156            position.y = avg.y;
157
158        })
159    }
160  });
161
162  return (
163    <>
164        <group ref={groupRef}>
165            {[1,2,3,4,5,6].map((item, index) => {
166                return ( 
167                    <mesh>
168                        <sphereGeometry args={[0.05, 24, 24]} />
169                        <meshBasicMaterial color={"red"} />
170                    </mesh>
171                )
172            })}
173        </group>
174        <points ref={pointsRef}>
175        <bufferGeometry>
176            <bufferAttribute
177            attach="attributes-position"
178            array={new Float32Array(numPoints * 3)}
179            itemSize={3}
180            count={numPoints}
181            />
182            <bufferAttribute
183            attach="attributes-color"
184            array={new Float32Array(numPoints * 3)}
185            itemSize={3}
186            count={numPoints}
187            />
188        </bufferGeometry>
189        <pointsMaterial size={10} vertexColors />
190        </points>
191    </>
192  );
193}
194
195function SectionLines({ boxSize }) {
196    const horizontalDivisions = 2; // Number of horizontal sections
197    const verticalDivisions = 3;   // Number of vertical sections
198  
199    const horizontalStep = boxSize / horizontalDivisions;
200    const verticalStep = boxSize / verticalDivisions;
201  
202    const lineMaterial = new THREE.LineBasicMaterial({ color: 'black' });
203  
204    // Define lines for section boundaries
205    const lines = [
206      // Vertical lines
207      [
208        [-boxSize / 2, -boxSize / 2, 0],
209        [-boxSize / 2, boxSize / 2, 0],
210      ],
211      [
212        [-boxSize / 2 + verticalStep, -boxSize / 2, 0],
213        [-boxSize / 2 + verticalStep, boxSize / 2, 0],
214      ],
215      [
216        [-boxSize / 2 + 2 * verticalStep, -boxSize / 2, 0],
217        [-boxSize / 2 + 2 * verticalStep, boxSize / 2, 0],
218      ],
219      // Horizontal lines
220      [
221        [-boxSize / 2, -boxSize / 2, 0],
222        [boxSize / 2, -boxSize / 2, 0],
223      ],
224      [
225        [-boxSize / 2, -boxSize / 2 + horizontalStep, 0],
226        [boxSize / 2, -boxSize / 2 + horizontalStep, 0],
227      ],
228      [
229        [-boxSize / 2, -boxSize / 2 + 2 * horizontalStep, 0],
230        [boxSize / 2, -boxSize / 2 + 2 * horizontalStep, 0],
231      ],
232      // Right-hand exterior vertical line
233      [
234        [boxSize / 2, -boxSize / 2, 0],
235        [boxSize / 2, boxSize / 2, 0],
236      ],
237      // Bottom exterior horizontal line
238      [
239        [-boxSize / 2, boxSize / 2, 0],
240        [boxSize / 2, boxSize / 2, 0],
241      ],
242    ];
243  
244    return (
245      <>
246        {lines.map((line, index) => (
247          <line key={index} geometry={new THREE.BufferGeometry().setFromPoints(line.map(p => new THREE.Vector3(...p)))}>
248            <primitive object={lineMaterial} attach="material" />
249          </line>
250        ))}
251      </>
252    );
253  }
254
255function App() {
256  const boxSize = 1;
257  const numPoints = 50;
258
259  return (
260    <Canvas
261      orthographic
262      camera={{
263        zoom: 480,
264        position: [0, 0, 5],
265        near: 0.1,
266        far: 1000,
267      }}
268      style={{ height: "500px", width: "500px" }}
269    >
270      <color attach="background" args={["white"]} />
271      <Points numPoints={numPoints} boxSize={boxSize} />
272      <SectionLines boxSize={boxSize} />
273    </Canvas>
274  );
275}
276
277export default App;

2 points which need to be addressed:

Getting 3D centroids in real time
Moving from CPU to GPU to take advantage of parallel processing power

Moving to the GPU will be tricky as state management is non existent apart from raw maths and deterministic calculations.

Centroids - Precursor to Normal Calculation in Point Clouds

More articles from theFrontDev

Crafting a Spatially Expanding Blob in Three.js - Dynamic Geometry and Bounding Box Alignment

Visualizing a 3D Sphere with Convex Hull and Wireframe Using R3F.